
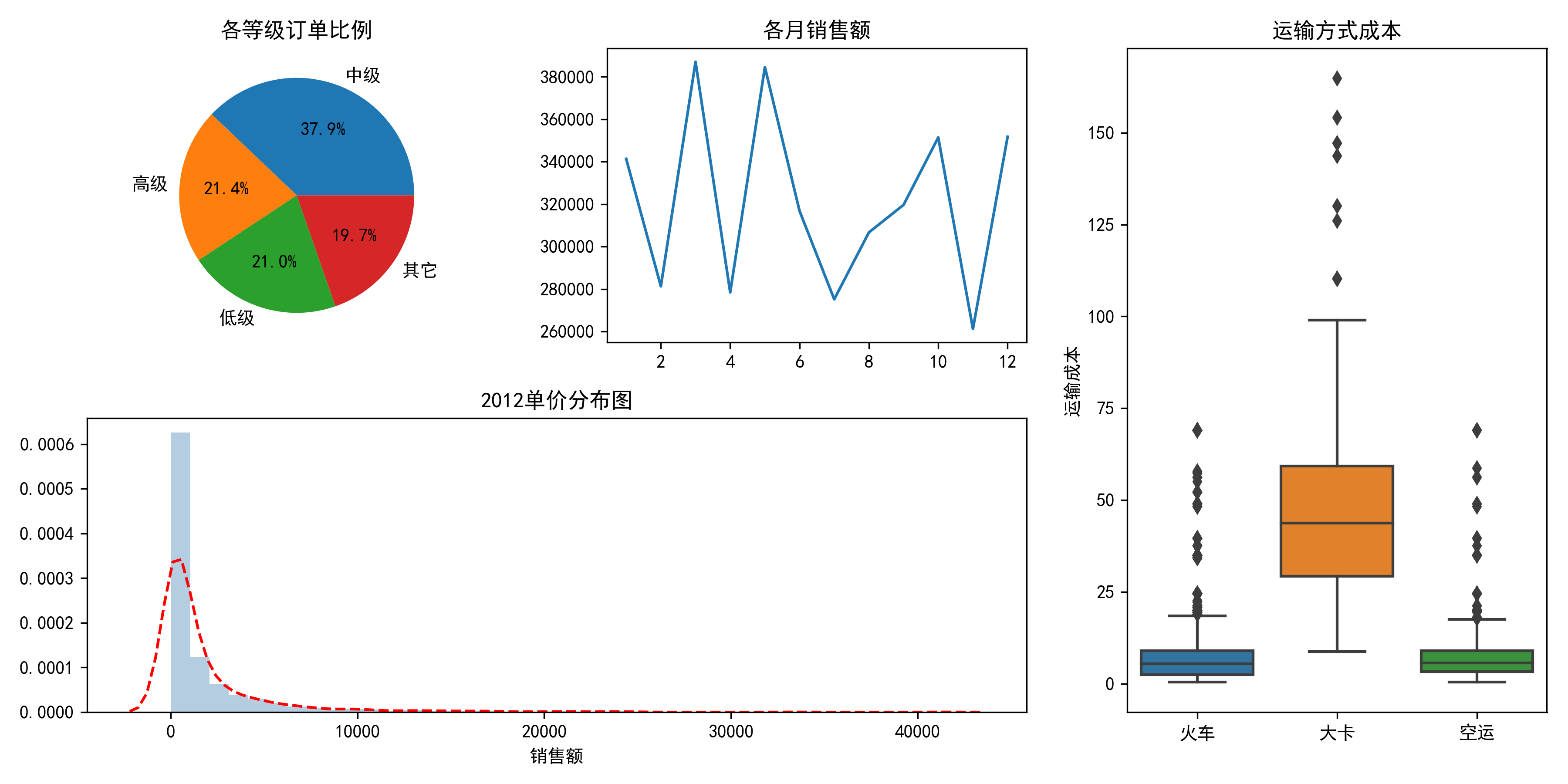
Question 3: What is the difference between plt.subplots() and plt.figure() The combination of the correct Locator and Formatter gives very fine control over the tick locations and labels. The location of the ticks is determined by a Locator object and the ticklabel strings are formatted by a Formatter. They take care of setting the graph limits and generating the ticks (the marks on the axis) and ticklabels (strings labeling the ticks). These are the number-line-like objects (circled in green). Each Axes has a title (set via set_title()), an x-label (set via set_xlabel()), and a y-label set via set_ylabel()). The Axes contains two (or three in the case of 3D) Axis objects (be aware of the difference between Axes and Axis) which take care of the data limits (the data limits can also be controlled via set via the set_xlim() and set_ylim() Axes methods). A given figure can contain many Axes, but a given Axes object can only be in one Figure. This is what you think of as a plot, it is the region of the image with the data space (marked as the inner blue box). In the context of matplotlib, axes is not the plural form of axis, it actually denotes the plotting area, including all axis. Question 2: Difference between “axes” and “axis” in matplotlib? This window will be just divided in 4 parts with my example.įigure2, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2) This plot 4 figures which are named ax1, ax2, ax3 and ax4 each one but on the same window. Or you can plot multiple figures like this: fig1, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2) Plot one or several figure(s) in the same window If you just want to get one graphic, you can use this way. Plot just one figure with (x,y) coordinates plt.plot(x, y) fig1, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2)Īfter reading through a bunch of stackoverflow explainations, I compiled them here: Question 1: What is the difference between drawing plots using plot, axes or figure in matplotlib? Play around with different parameter settings for each of the distributions to see how these change the properties of the distribution.When working with python libraries, especially for visualization, I usually get confused my number of options available for plotting. Set figure size, give it a name and save the figure (Ironically, if you don’t specify this, the subplots are squeezed together even more tightly and text is overlaid.)
Give the figure a tight_layout so that subplots are nicely spaced between each other. Count from row 2 column 2, do the following …

Specify the location of the second small subplot: start counting from row 1 column 2. In this subplot, do the following (similar to above) … Specify the location of the first small subplot: start counting from row 0 column 2.
Call the function gridspec.Gridspec and specify an overall grid for the figure (in the background).
Create a figure object called fig so we can refer to all subplots in the same figure later. # Plot figure with subplots of different sizes
#ADD SUBPLOT MATPLOTLIB HOW TO#
You will get the hang of how to specify different parameters quickly:
#ADD SUBPLOT MATPLOTLIB CODE#
The code to generate subplots is long but repetitive. Now we can plot these data in a single figure, which will have 1 large subplot on the left, and a column of 3 small subplots on the right. Get 1000 samples from a chi-square distribution with 2 degrees of freedom. The F distribution typically arises in an analysis of variance (ANOVA), which compares within-group to between-group variance this comparison depends on sample size, which determines degrees of freedom in the numerator dfnum and denominator dfden. Get 1000 samples from a t distribution with 29 degrees of freedom. Get 1000 samples from a normal distribution with mean 0, standard deviation 1. Include this line if using an IPython/ Jupyter notebook. # Import libraries import numpy as np import matplotlib.pyplot as plt import idspec as gridspec %matplotlib inlineĭist_norm = np.


 0 kommentar(er)
0 kommentar(er)
